Please Use Internet Explorer 5
or Over.
Ó Copyright 2004 by
Author’s E-mail address:
yaoyanyy2000@yahoo.com.au
3A.
Entity Field Electromagnetism (Part A)
Contents
3.2.
Electric Force Field and Electric Action E
3.3. Electric Potential Energy
Note:
As I mentioned before that an entity field has to be introduced back into classical physics so that an electron has a virtual photon with it. This means that the newly defined electron has a particle and en entity field in its structure. An electromagnetism based on this kind of electron is called entity field electromagnetism. Comparing with classical physics, all the formulae are unchanged, but the concepts of modern physics are merged in entity field electromagnetism right form the beginning.
3.1. Entity Electric Field
In our earth confined physical world, there are three kinds of common elementary particles: electron e, proton p and neutron n.
The definition of an electron has to define both its particle and its entity field. That is:
An electron
possesses two physical essentials: (1) It has unit particle with a rest mass of
Me=9.109X10-31 kg. (2) It has unit entity electric field with an
electric charge of e=–1.6X10-19
C. The
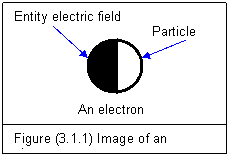
image of an electron is shown in figure (3.1.1). The two parts of an
electron are equally important and can not be separated so far.
Both particle and entity electric field of an electron are entities. They obey laws of conservation of matter and energy. There are other related conservation laws such as mass conservation, mass-energy conservation and electric charge conservation, etc.
A proton also possesses unit particle and unit entity electric field. The rest mass of its particle is Mp=1.673X10-27 kg. The electric charge of its entity electric field is +e=1.6X10-19 C. Both particle and the field of a proton are joint entities.
Figure (3.1.1) can also be used for the image of a proton. The differences are that its particle is heavier and bigger, and its entity electric field has unit positive charge.
Electron or
proton satisfies
(3.1.1)
Where Ma and Mb are the masses of any two particles A and B; r is the distance between the two.
Electron or proton has electric force due to the electric charge of its entity electric field. This force obeys Coulomb’s law and can be expressed as
(3.1.2)
Where qa and qb are the charges of any two particles A and B; r is the distance between the two.
The rules for electric force between charges are: Like charges repel; unlike charges attract. For our convenience, we define a direction of electric force to be from positive pointing to negative. There is no real direction of electric force in the physical world.
If an electron runs into a proton, the electric forces attract each other and combine the two particles into a compound particle—neutron.
The image of a neutron is shown in figure (3.1.2).
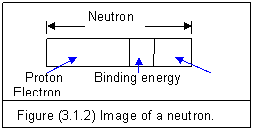
The binding energy Eb is transformed from the masses of e and p. The mass-energy conservation is
(3.1.3)
The rest mass of a neutron is Mn=1.675X10-27 kg. It is less than the sum of Me and Mp due to the existence of binding energy Eb.
There is no way to combine an electron and a neutron into a proton.
Once an electron and a proton form a neutron, their entity electric fields are confined within the compound particle so that it appears electric neutral. This means that the force of an entity electric field from single electron or proton is one to one based force. This force can not be represented by vector and can never be resolved into components.
Because all
objects in the world are made of electron, proton and neutron, they all obey
A system containing an equal number of electrons and protons appears electric neutral due to the forces of its entity electric fields are interacting within the system. This means that any atom, molecule or object contains large number of entity electric fields no matter we can detect them or not.
If an electron and a proton form a stable system, their electric field forces only interact between the two particles. A third electron e3 cannot join the system and share the interacting forces if it is far away from the system (L>>r). This is shown in figure (3.1.3).
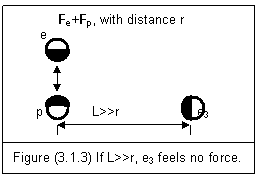
If the third electron has enough energy to overcome the binding energy of the system and reaches a distance L<r, it will form a new system with the proton, and the first electron will be set free. This is shown in figure (3.1.4). During this process, we can only detect one electron and one electric neutral system.
An electric charge refers to an object that has unbalanced numbers of electrons and protons. Each excessive electron or proton contributes a unit charge to the electric charge. It is positively charged if it has excessive protons, or negatively charged if it has excessive electrons.
Any charged object contains large number of excessive unit charges.
An interaction
between two charged object is the resultant interactions of all unit charges
involved; therefore, the force of a charged object can be represented by a
vector F and can be resolved
into components.
(3.1.4)
Where r12 is vector distance between q1 and q2 pointing from q2 to q1; and e0 is the permittivity of free space. As a matter of fact, the vector F is much more helpful when dealing with three or more charged objects.
3.2. Electric Force Field and Electric Action E
Although an entity electric field coexists with every elementary particle of an object, it does not show any electric force if the object has balanced number electrons and protons.
To charge an object is to make its number of electrons and protons unbalanced so that it has excessive electric force to act on other objects. To describe this excessive electric force, we can imagine that there is an electric force field around a charged object. This electric force field was misunderstood in classical physics as electric field. In fact, it is not an entity but an abstract concept for the study of electric force.
By putting a test charge q0 into an electric force field, we can check out the electric force on q0. Thus, we can introduce an electric action E to describe the strength of an electric force field. It is defined as the ratio between the force F on the test charge q0 at that point and the charge of q0
(3.2.1)
Here we find that an electric action E is a vector, which has the same direction as an electric force F. From this definition we know that, in classical physics, the E was called electric field intensity by mistake.
Equations (3.1.4) and (3.2.1) can be rearranged as
(3.2.2)
Here r0 is the unit vector of r.
As for a group of three or more charges, the combined electric action can be expressed as
(3.2.3)
Again, to simplify the problem, we can imagine that there are electric force lines around an electric charge. As a tradition, we define the direction of the lines are from positive charge pointing to negative charge. This is shown in figure (3.2.1).
Figure (3.2.1) Electric
force lines. + - Electric force lines Electric force lines of a positive charge of a negative charge
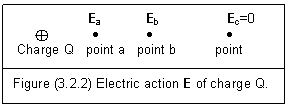
Now, let’s recheck the example of electric action E caused by a charged object. Figure (3.2.2) is the same picture as figure (2.1.1) but with entity meaning.
The positive charge Q means that this object has excessive proton and can form a positive electric force field around it. Since point a is closer than point b, it can feel stronger electric force. So, we have
Ea>Eb (3.2.4)
As for point c® ¥, we can get
Ec=0 (3.2.5)
The entity electric fields in the structure of Q remain unchanged to form the source of the E.
Similarly, we can recheck the problem of figure (3.2.3). This is the same situation as shown in figure (2.1.2)
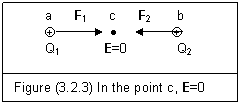
Suppose Q1=Q2. Q1 is at point a, Q2 is at point b. The test change is put at the middle point c. Electric force on point c is
F=F1+F2=F1-F2=0 (3.2.6)
This means that F1 and F2 are counteracted. The electric action at point c can also be calculated as
E=E1+E2=E1-E2=0 (3.2.7)
These zero results of Equations (3.2.6) and (3.2.7) have nothing to do with the entity electric fields of Q1 and Q2. There is no violation of conservation laws.
If we define electric action flux j as the density of electric action through a surface A, the increment of Dj is
Dj=E·nDA=
Where n is unit normal vector of the surface
A. q is the angle made by E and n. For a
close surface, the total flux of electric action is
(3.2.9)
For a group of charges, equation (3.2.9) can be expressed as
(3.2.10)
In which SQin is the summary of all charges inside.
For a continuously charged object, we have
(3.2.11)
In which r is volume charge density.
For an object with charge Q, we simply have
(3.2.12)
Equations (3.2.10), (3.2.11) and (3.2.12) told us that the source of electric action E is electric charge Q. This is to say that if a close surface has net electric action flux through, there are excessive entity fields inside the surface.
3.3. Electric Potential Energy
Work can be done by an electric force since it can move other charged particles. If a charge q is moved a distance S, the work done by electric force is
W=F·S=qE·S (3.3.1)
We can see that both E and F are connected with work, so E can also be thought as the source of work.
If a point charge q is put in the electric force field of charge Q, the point charge tends to move. This means that the charge q has potential energy. If the distance between the two is r, electric potential energy U is
(3.3.2)
If the point charge q is moved from point A to point B, the work done by electric force of Q is
(3.3.3)
Because the excessive entity electric fields in the structure of charge Q produce electric force field, this force field will exist with or without the present of the point charge q. Thus, an electric potential f can be introduced for our convenience. It is defined as the ratio between electric potential energy U and the value of point charge q
(3.3.4)
In which q®0 is to eliminate the affect from its entity field.
For a group of point charges, equation (3.3.4) should be expressed as
(3.3.5)
For an object with continuous charge distribution in a volume, we have
(3.3.6)
Combining equations (3.3.4) and equation (3.2.2) we can get
the relationship between electric potential f and electric action E
(3.3.7)
In this equation, if the path of
is from point A,
passing a point B and back to point A again, there is
(3.3.8)
This is to say that the electric action E is a conservative quantity. This is easy to be understood when thinking of the E is defined to represent electric force F. Thus, electric action can be expressed as
(3.3.9)
Comparing with classical physics one can find that all the equations so far are unchanged but with entity meanings. Entity field brings us a clear picture of physical world. No more contradictories. No more ambiguities.
3.4. Conductor
A conductor can conduct electricity and heat easily. This is to say that electric current can flow through a conductor with little resistance.
All metals are good conductors. In a solid metal, each atom gives up one or more electrons from its outer shell easily to become free electrons. An electric potential established at both ends of a conductor can cause free electrons and make them move towards the positive end. This forms a current flow in the conductor. To keep the current flow, a power supply should be connected to supply new electrons to the negative end and to move arrived electrons from the positive end.
Considering a conductor slab is placed into an external electric force field as shown in figure (3.4.1). Free electrons are attracted to the anode and accumulated at surface a. Electrons from nearby atoms will fill up the vacancies caused by free electrons. The resultant of this movement leaves an equal amount of positive charge accumulated on surface b.
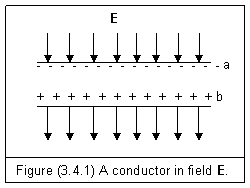
As we know that electric force of an electron or a proton is one to one based force. If the negative charge at surface a is interacting with anode, and the positive charge at surface b is interacting with cathode, there is no interaction between surfaces a and b. So, we have
(Inside
conductor) (3.4.1)
Let’s examine the surface a in figure (3.4.1). Since electric action E is caused by entity electric field, it is in proportion to the number of electrons, it is also in proportion to the surface charge density. If the external field is at normal direction of the surface a, and the surface charge density is s, we have
(3.4.2)
and
Et=0 (3.4.3)
This means that the interaction of electric force is along the direction of electric force field. There is no electric action E in the direction perpendicular to it.
Let’s consider the infinite parallel-plate
conductors a and b in figure (3.4.2). If the surface
charge density is s0, electric field action En
between the two plates is
(3.4.4)
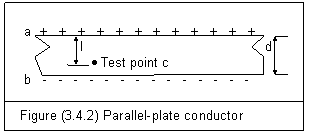
Within the plates a and b, there is a test point c with a distance l. Electric action potential f at point c can be calculated by equation (3.3.7)
(3.4.5)
If V is denoted as electric potential different, d is the distance between the two parallel-plates, V can be expressed as
(3.4.6)
Comparing equation (3.4.6) and equation (3.4.4), we can get
V=Ed (3.4.7)
If a point charge q with a rest mass of m is put into an electric action E, an electric force will exert on the charge and make it accelerate. (Please see figure (3.4.3)).
Suppose the initial state of the charge q is at rest, the force acting on it is
The acceleration a then can be expressed as
(3.4.9)
If charge q is moved from point a to another point b, the work done by electric force is
Wab=F(b-a)=qE(b-a) (3.4.10)
Combining equation (3.4.7) with equation (3.4.10) we have
Wab=qVab (3.4.11)
If the charge q is finally reached a speed v, its kinetic energy equals the work done by electric force F. There is
(3.4.12)
3.5. Parallel-plate Capacitor
Figure (3.4.2) is also known as parallel-plate capacitor. Its surface charge density s is the ratio of total charge Q and the total area A of the conductor. Thus, equation (3.4.4) can be expressed as
(3.5.1)
From equation (3.5.1) and equation (3.4.7): V=Ed, we have
(3.5.2)
Where the three constants: area A, distance d and permittivity e0 can be replaced by a new constant called capacitance C
(3.5.3)
Where C0 means that there is a vacuum between its plates. So, equation (3.5.2) can be simplified as
Q=C0V (3.5.4)
In normal state, a capacitor does not have any charge. The charge is performed by an external force to move electrons from one plate to the other. Thus an electric force field is established and causes an electric action potential f between the two plates. In this process, the work done by the external force is changed into electric potential energy of the capacitor.
To find out the energy of the capacitor, let’s consider that an electric charge q is moved in a charged capacitor by an external force. The work done by the external force is equal to the consumed energy to overcome the electric action. That is
(3.5.5)
Total energy of the capacitor is
(3.5.6)
Considering equations (3.5.1), (3.5.3) and (3.5.4) we can get
(3.5.7)
For a parallel-plate capacitor, its area A times distance d makes the volume between the two plates. So, electric energy density w can be introduced and is defined as w=W/Ad. Equation (3.5.7) then can be changed as
(3.5.8)
In figure (3.5.1), there are two capacitors in series.
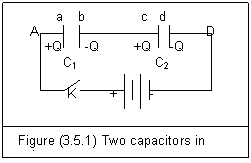
If electric force field of the battery charges plate a of C1 with Qa, the charge on plate b is: Qb=-Qa. Because the plate b of C1 is connected with the plate c of C2, the charge on plate c is opposite to that of plate b. That is: Qc=−Qb=Qa. Then, plate d has: Qd=-Qa. So, we get
Q1=Q2=Q (3.5.9)
Electric potential different across the series is
(3.5.10)
In which C is equivalent capacitor. This result can be used for three or more capacitors in series. The equivalent capacitor is
(3.5.11)
Figure (3.5.2) shows two capacitors in parallel.
In this situation, capacitors C1 and C2 have the same electric potential different across A and D. We have
V1=V2=VAD (3.5.12)
Battery charges C1 and C2 separately and the total charge is
Q=Q1+Q2=C1V1+C2V2=(C1+C2)V=CV
(3.5.13)
In which C is equivalent capacitor. For many capacitors in parallel, there is
C=C1+C2+C3+∙∙∙+CN (3.5.14)
3.6. Dielectrics
Capacitance C0 is valid only when there is a vacuum between the plates. If a dielectric is inserted in between, the capacitance C will be increased by a factor er called relative permittivity
C=erC0 (3.6.1)
There is er>1 for all dielectrics. On the other hand, with dielectric presented, electric action E is smaller than which of vacuum situation E0, That is
(3.6.2)
The increment of capacitance and the decrement of electric action is due to that the external electric action E is partially used to interact with the electric action of dielectric.
The molecular structure of dielectric decided that there is no free electron can be moved by external electric action. If the potential difference is high enough to move electron out of its structure, this dielectric is damaged. This is known as break down.
There are two kinds of dielectrics due to two different kinds of molecular structures. One has permanent electric dipole moments P0, and the other hasn’t. This is because that the molecular structure of some dielectrics has certain degree of electric charge in nature. This kind of dielectric is called polar molecule dielectrics. For the other kind of dielectrics, their molecular structure does not have any electric charge in nature; they are called non-polar molecule dielectrics.
In normal state, all molecules are random arranged, so both kinds of dielectrics have no electric action.
If a dielectric of non-polar molecules is put into an external electric action, the electric forces of its electrons and protons will interact with the external electric action. The resultant effect makes the electrons tend towards anode. This makes non-polar molecules appear polarized. If p is denoted as electric dipole moment of one polarized molecule, the total electric dipole moment of dielectric P can be expressed as
P=np (3.6.3)
Where n is the number density of polarized molecules. The stronger the external electric action is the more molecules will be polarized.
If a dielectric of polar molecules is put into an external electric action, the charges of polar molecules will interact with the external electric action. The rule of this interaction is: Like charges repel and unlike charges attract. The resultant is to make random polar molecules align with the external electric force field. If p0 is denoted as permanent electric dipole moment of one molecule, the total electric dipole moment P is
P=np0 (3.6.4)
Where n is the number density of aligned polar molecules.
In general, for either non-polar molecules or polar molecules of dielectrics, the effect of external electric action is always tending to align polarized molecules or polar molecules with its action E0. This is shown in figure (3.6.1).
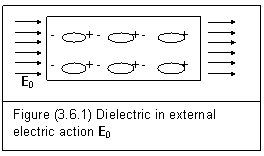
This alignment cannot affect all molecules due to the interaction between electron and proton, and thermal agitation. Within the dielectric, entity field action of a polar molecule or polarized molecule is counteracted by the action of another molecule next to it. At both side of the dielectric, a surface charge is established to interact with the external electric action E0
Figure (3.6.2) is a simplified picture to show the surface charge of a dielectric.
Due to the surface charges at both sides, inside the dielectric, electric action E is weaker than E0.
The surface charge density of the dielectric is denoted as sp and is defined as
sp=P·n0 (3.6.5)
Here n0 is the unit normal vector of dielectric surface. This surface charge density sp can be thought as the counter part of the capacitor’s surface charge density s, which forms external electric action E0. Inside the dielectric, total contribution of the two charge densities is: s-sp. Equation (3.5.1) then can be changed to express the electric action inside
(3.6.6)
The direction of E is in the same direction of E0.
Equation (3.6.6) can be changed as
sp=s-e0E (3.6.7)
By using equation (3.6.2) and equation (3.5.1), equation (3.6.7) can be changed as
(3.6.8)
From figure (3.6.2) we can see that, inside the dielectric, E and P are in the same direction. Thus, in the direction of E, equation (3.6.5) can be written as
sp=P (3.6.9)
Then, equation (3.6.7) can be expressed as
(3.6.10)
Combining equation (3.6.2) with equation (3.6.10), we have
(3.6.11)
To simplify the calculation, we can use a symbol c as electric susceptibility to replace er-1. That is
c=er-1 (3.6.12)
Then, equation (3.6.11) is expressed as
(3.6.13)
From equation (3.6.10), we can also get an expression of surface charge density s
s=e0E+P (3.6.14)
This means that the surface charge density of a capacitor is the reason of electric action E and electric dipole moment P within a dielectric.
Since the total charge of capacitor is the integral of its electric charge density s over the whole area s
(3.6.15)
Comparing with equation (3.2.9), the right side of equation (3.6.15) can be understood as electric action flux of dielectric.
If we introduce a electric displacement D as
D=e0E+P=e0erE=eE (3.6.16)
Equation (3.6.15) can be re-written as
(3.6.17)
For a continuously charged dielectric, we have
(3.6.18)
We need to emphasize that the displacement D is not an entity electric field. It is a vector symbol of electric force field to be used to simplify dielectric problem. Entity electric field coexists with every elementary particle no matter we can detect it or not.
With the concept of electric displacement D, electric energy density of any capacitor can be expressed as
(3.6.19)
3.7. Current and Resistance
When a constant electric potential different is applied on the ends of a conductive wire, electric action will make free electrons move continuously along the wire and form a steady electric current. The direction of the moving electrons is from negative end to positive end. But the direction of current, by tradition, is defined from positive end to negative.
If a net charge Dq passes through the cross-sectional area of a conductor in a time period of Dt, electric current I is defined as the ratio between Dq and Dt
(3.7.1)
With a steady power supply, we can get a constant electric current flow. In this situation, a current density J is used and is defined as electric current dI through cross-sectional area dA
(3.7.2)
Here n0 is unit normal vector of the cross-sectional area. This is shown in figure (3.7.1).
Figure (3.7.1) Current density J. N0 J I
Cross-sectional area
Since moving electrons form an electric current, any interference can cause a resistance to individual electron and then affect the current. Thus, a current is only related to the average speed of electrons.
Figure (3.7.2) shows free electrons moving in a conductor.
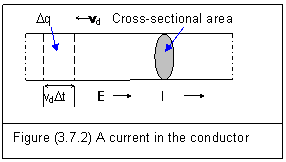
If the average speed of free electrons is vd and the area of the cross-section is A, the charge passing this cross-sectional area is
Dq=envdADt (3.7.3)
Where n is number density of free electrons. By using equation (3.7.3), equation (3.7.1) can be changed into
(3.7.4)
We can find in figure (3.7.2) that the direction of current is opposite to which of moving electrons.
Comparing equation (3.7.4) with equation (3.7.2) we have
J=-envd (3.7.5)
To calculate the average speed of free electrons vd, we suppose that a free electron is initially at rest and then accelerated by an electric action E to a speed v
v=at (3.7.6)
Considering equation (3.4.8), equation (3.7.4) can be expressed as
(3.7.7)
In fact, a free electron does not move freely in the structure of a conductor. The average speed vd can be considered to be half of the maximum speed v. That is
(3.7.8)
Where t is the average moving time of free electron. Combining equation (3.7.8) with equation (3.7.5), we can get
(3.7.9)
Since the ratio between J and E is constant for a certain conductor, it can be understood as conductivity s
(3.7.10)
Then, resistivity r is the inverse of conductivity s
(3.7.11)
Thus, equation (3.7.9) can be expressed as
(3.7.12)
In the real situation, resistivity r is not a constant. It will increase as the increment of the conductor’s temperature. The main reason is that once electron is accelerated by an electric action E, its entity electric field is also accelerated. During this acceleration, the particle of the electron gained kinetic energy while the entity electric field of which gained extra entity field energy as entity magnetic field. If this moving electron collides with other electrons, the particle is decelerated to lose kinetic energy while its entity magnetic field is released as electromagnetic wave or heat.
Higher temperature of a conductor means more collisions occurred to its free electrons. Thus, the average moving time t is reduced and the conductor has higher resistivity. We can understand better after studying entity magnetic field and entity field electromagnetic wave later.
For a conductive wire in normal situation, its resistance R is the ratio between potential difference V of both ends and electric current I though it. This is Ohm’s law
(3.7.13)
The resistance of a conductor also depends upon three factors of the material: resistivity r, length L and its cross-sectional area A. There is
(3.7.14)
Ohm’s law is an empirical relationship but it works well for most metals under a wide range of circumstance.
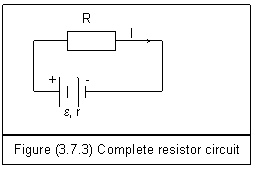
Figure (3.7.3) is a complete circuit including a resistor and a battery. The battery has electromotive force ℰ and internal resistance r. From Ohm’s law, we can get
ℰ=Ir+IR (3.7.15)
As an electric current passes a resistor, electric energy is transformed into other kinds of energies such as heat, light and mechanical energy.
Suppose an electric potential different V moves a charge dq through a resistor, the work done by its electric force is decided by equation (3.4.11) as
dW=V·dq (3.7.16)
As we know that power is defined as
the rate at which work is being done
(3.7.17)
Thus, we can get power dissipated from
a resistor
(3.7.18)
In which equation
(3.7.1) is used. By using Ohm’s law of equation (3.7.13), equation (3.7.18)
can be changed to
(3.7.19)
Figure (3.7.4) is three resistors in parallel.
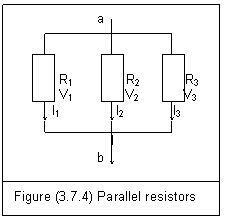
The potential difference across every resistor equals Vab
Vab=V1=V2=V3 (3.7.20)
The total current I is divided into three and passes through each resistor branch
I=I1+I2+I3 (3.7.21)
By applying Ohm’s law of equation (3.7.13), we have
(3.7.22)
Where R is equivalent resistance
(3.7.23)
In general, the reciprocal of the equivalent resistance of a set of resistors connected in parallel is equal to the sum of the reciprocals of the individual resistances
(3.7.24)
Figure (3.7.5) is three resistors in series.
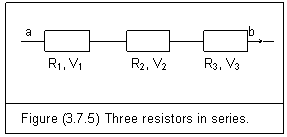
An electric current I passes through every resistor. The total potential difference Vab is the sum of the potential differences across each resistor
Vab=V1+V2+V3 (3.7.25)
By using Ohm’s law of equation (3.7.13), this equation can be changed as
IR=IR1+IR2+IR3 (3.7.26)
Here R is equivalent resistance. Dividing it through by current yields
R=R1+R2+R3 (3.7.27)
In general, equivalent resistance of a set of resistors connected in series is equal to the sum of the individual resistance
R=R1+R2+R3+···+RN (3.7.28)