Please Use Internet Explorer 5
or Over.
Ó Copyright 2004 by
Author’s
E-mail address: yaoyanyy2000@yahoo.com.au
4.
Entity Field Optics
Contents
4.2.
Entity Field Electromagnetic Wave
4.3.
Basic Characteristics of an Independent Entity Field
4.4.
Propagation of Independent Entity Field in Transparent Medium
4.5.
Property Wave Superposition
4.8. Wrong Concept of
Polarization of Light
Note:
Due to historical reasons, optics divided into three parts: geometrical optics, in which light is treated as straight ray; wave optics, in which light is electromagnetic wave; quantum-optics, in which light is photon or particle.
Since wave optics is based on the wrong definition of electric and magnetic fields, it is a wrong theory made of many wrong concepts.
In this chapter, we will use entity field theory to rebuild an optics called entity field optics. In this entity field optics, all straight ray, wave and particle of light are unified as independent entity field.
4.1. Independent Entity Field
In entity field electromagnetism, entity field coexists with its elementary particle. Since this entity field is fixed to its particle, it can be called dependent entity field.
If an electron is decelerated, its entity magnetic field is released as photons carrying electromagnetic wave. This means that the building material of a photon can only be an entity field. Since this released entity field exists in space by itself, it becomes independent entity field.
Independent entity field differs from dependent entity field in many ways. Most importantly, it travels with speed c in free space. Thus, the study of independent entity field is quite different from the study of dependent one.
To deal with independent entity field, Maxwell’s equations (3.15.5)—(3.15.8) must be changed into
(4.1.1)
(4.1.2)
(4.1.3)
(4.1.4)
As we can see that there is no depending source for either E or B. Consequently, there are other three important changes:
(1) Equation (4.1.3) says that a time-varying B becomes an E; equation (4.1.4) says that a time-varying E becomes a B. Both B and E can only exist by changing into each other. Yes, both of them are quantified and neither of them can form a complete wave by itself.
(2) The two symmetrical equations (4.1.3) and (4.1.4) indicate that either B or E takes equal length of the interchange period between the two. This means that each of them takes half of a period.
(3) Since B and E are independent of any source, they are no longer vectors. For the same reason, they have constant moving speed c according to special relativity. The reference system they attached on must also have constant moving speed c. This means that the natural reference system of equations (4.1.1) to (4.1.4) is a light speed reference system. The wave described by equation (4.1.3) and (4.1.4) is a wave on top of this light speed reference system.
A correct understanding of electromagnetic wave must be based on correct understanding of above three requirements of independent entity field.
4.2. Entity Field Electromagnetic Wave
From equations (4.1.1.)—(4.1.4) we can get wave equations of entity field electromagnetic wave. On eliminating the magnetic action B by combining equation (4.1.3) and equation (4.1.4), after taking their curl, we find
(4.2.1)
Since equation (4.1.1) requires Ń·E=0, then we have
(4.2.2)
This is homogeneous wave equation of electric action E with respect to its independent entity field in light speed reference system.
If the electric action E is eliminated form equation (4.1.3) and equation (4.1.4), magnetic action B also satisfies the same equation
(4.2.3)
This is homogeneous wave equation of magnetic action B with respect to its independent entity field in light speed reference system.
Equations (4.2.2) and (4.2.3) give us a false idea that either electric action E or magnetic action B can form a continuous wave. This is contradictory to Maxwell’s equations (4.1.3) and (4.1.4). The reason for these mistakes is that when we eliminate magnetic action B from equations (4.1.3) and (4.1.4), we are taking the B out and filling its space with E. Due to the disappearance of B and the doubled amount of E, originally quantified E and B become a continuous E. Thus, this correct mathematical procedure produced incorrect physical results. The same mistake occurred when eliminating E. To correct these mistakes, we have to modify wave equations (4.2.2) and (4.2.3) to meet the requirement of Maxwell’s equations (4.1.3) and (4.1.4).
In entity field theory, the E marks its entity field has electric property and the B marks its entity field has magnetic property. Both E and B can be unified as the property P of an entity field. In this unification, electric action E is understood as electric property PE, and magnetic action B is understood as magnetic property PB. Then, equations (4.2.2) and (4.2.3) can be unified as
(4.2.4)
This is the only valid wave equation of independent entity field with correct physical meaning.
Equation (4.2.4) means that the speed of property wave is c with respect to its independent entity field, on the condition that the reference system is fixed to the independent entity field. Since independent entity field travels with speed c in ordinary inertial reference system, equation (4.2.4) can no longer be used to describe its property in any ordinary inertial reference system.
For a light speed reference system in which an independent entity field is stationary along its X-axis. The simple harmonic wave solution of equation (4.2.4) is
(4.2.5)
In which l is known as the wavelength.
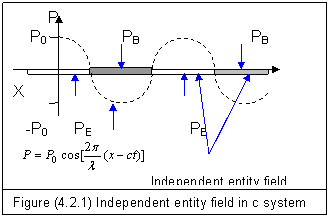
From equation (4.2.5), a model of independent entity field can be achieved as shown in figure (4.2.1).
In this picture, the speed of independent entity field is zero in light speed reference system while its property waves with speed c along positive X-axis. There is no zero point for entity field. There are zero points for its property wave. Conservation laws are valid at any position and at any time.
As the property P waves to its positive value, its independent entity field has electric property PE and demonstrates electric action. As the property P waves to its negative value, its independent entity field has magnetic property PB and demonstrates magnetic action. Thus, the whole independent entity field is quantized into electric entity fields and magnetic entity fields. Equation (4.2.5) then can be expressed as
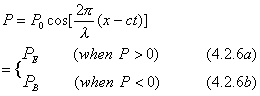
From this equation we can get
PE=-PB or PE+PB=0 (4.2.7)
Which means that electric property PE is opposite to magnetic property PB.
Our discussion so far is only bound with the natural reference system of equation (4.1.1)—(4.1.4), which is light speed reference system. In reality, nobody can stand on light speed reference system due to special relativity. To have a better understanding of electromagnetic wave, equation (4.2.6) has to be transformed into ordinary inertial reference system. Again, due to special relativity, independent entity field travels with a speed c in any inertial reference system, Galilean coordinate transformation equations have to be used to perform the required reference frames’ transformation.
Figure (4.2.2) Inertial
frame K and c frame K’
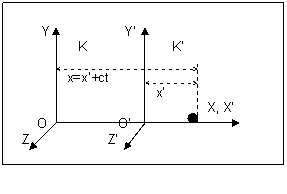
There are two reference frames K and K’ in figure (4.2.2). K is an ordinary inertial frame and K’ is a light speed one. We suppose that K’ moves along the X-axis of K and at the time t=0 in both frames, their origins coincide. At the time t, Galilean transformation equations give
x=x’+ct (4.2.8)
y=y’ (4.2.9)
z=z’ (4.2.10)
And time equation
t=t’ (4.2.11)
And velocity equation
v=v’+c (4.2.12)
For a stationary independent entity field in K’ frame along X’-axis, its property wave is
(4.2.13)
In K frame, the x’ of equation (4.2.13) has to be replaced by the x of equation (4.2.8). That is
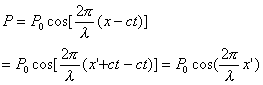(4.2.14)
The velocity of the independent entity field in K’ frame is given by equation (4.2.12)
v=v’+c=c (4.2.15)
Where v’=0 is the speed of independent entity field in K’ frame.
Checking equation (4.2.14), x’ is the distance between O’ and x’, so, it can be replaced with a symbol l, thus, independent entity field in ordinary inertial reference system is
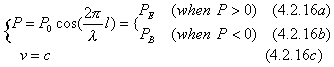
It means that, in any inertial reference system, an independent entity field travels with a speed c while its property changes with sine-shaped pattern. If we exam the property only, the combination of these two motions is known as property wave with respect to its entity field.
Based on equation (4.2.16), a model of independent entity field in ordinary inertial reference system is given in figure (4.2.3). As we can see that the whole independent entity field is quantized into entity electric fields and entity magnetic fields.
If an independent entity field is traveling in a medium, equation (3.15.5)—(4.15.8) should be written as
(4.2.17)
(4.2.18)
(4.2.19)
(4.2.20)
From equations (4.2.19) and (4.2.20) we
can get two wave equations
(4.2.21)
(4.2.22)
As we discussed before that equations (4.2.21) and (4.2.22) have to be combined as one property wave equation
(4.2.23)
Thus, the speed of property wave with respect to its independent entity field is
(4.2.24)
Its property wave then can be expressed as
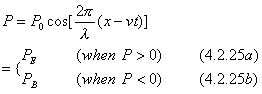
In which speed v is also the speed of reference system fixed to its independent entity field.
In ordinary inertial reference system, the independent entity field can be expressed as
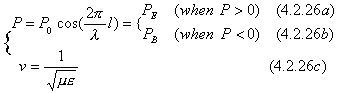
We can see that the speed of an independent entity field is dropped to v<c in a medium. Again, its property can be understood as an electromagnetic wave both in light speed system and in any inertial system.
4.3. Basic Characteristics of an Independent Entity Field
From equation (4.2.16) and figure (4.2.3) we know that an independent entity field has straight ray, particle and electromagnetic wave characteristics in nature.
(1) Straight ray
Equation (4.2.16c) indicates that an independent entity field has a constant speed c in free space. Equation (4.2.26c) defines that it has speed v=1/(me)1/2 in a medium. According to Newton’s first law of motion, independent entity field must move along a straight line.
A single independent entity field can only form a single straight ray. A light beam or a radio signal contains large numbers of single rays.
Geometrical optics is a powerful tool for the study of lenses and other optical instruments. Since the concept of ray and all related theory are correct from the viewpoint of entity field theory, we do not have to repeat them here.
(2) Particle
Equation (4.2.16) decides that an independent entity field travels with speed c while its property changes from electric to magnetic and back to electric again alternatively. Thus, the whole independent entity field is quantified into electric photons and magnetic photons. The minimum existing unit of an independent entity field is a photon so that to fulfill the electric and magnetic change. The minimum length of an independent entity field is the length of PE or PB. From figure (4.2.3) we can see that PE or PB represent a quantum of independent entity field or a photon of light. For a long ray of independent entity field, the total number of photons must be an integer.
It is easy to identify that the wavelength l of the property wave is the sum of the lengths of an electric photon and a magnetic photon. If DE is used for the length of an electric photon and DB for the length of a magnetic photon, either of the two is half of a wavelength l
DE=DB=l/2 (4.3.1)
(3) Wave
Either in light speed system or in any inertial system, an independent entity field carries electromagnetic wave with it. The only difference is that, in ordinary inertial system, the change of the property and the motion of the independent entity field can be described separately.
The most important fact about this electromagnetic wave is that the wave is originated as a property wave while its independent entity field travels along a straight line. Under certain conditions, an independent entity field can act like wave due to the influence of its property wave. Any wave experiment of light is to interfere the property wave so that the wave characteristic of light can be shown.
One thing for sure that this electromagnetic wave is totally different with water wave or sound wave. Needless to say that wave optics is a wrong theory.
As we know that an independent entity field is divided into electric photon PE and magnetic photon PB. An electric photon has electric action E and a magnetic photon has magnetic action B. So, an independent entity field can have electric and magnetic interactions with external electric and magnetic actions. According to Newton’s first law of motion, the track of an independent entity field is straight line unless it is affected by another force. The basic idea of any wave experiment is to interfere the electromagnetic wave with an electric or magnetic force so that to change the track of its photons.
From equation (4.2.7): PE=−PB we know that electric property PE is opposite to magnetic property PB. As the result, the force caused by an electric photon FE is opposite to which caused by a magnetic photon FB.
If an independent entity field travels in a homogeneous external electric force field or magnetic force field, the track of its photons is a straight line due to the opposite contributions of its FE and FB. This is why a ray of light or a photon appears electric and magnetic neutral.
If an independent entity field travels in a heterogeneous electric or magnetic force field, its two opposite interactions caused by FE and FB cannot be completely balanced. The track of this independent entity field is then forced away from the straight line.
Figure (4.3.1) shows a typical heterogeneous electric and magnetic force fields at the sharp edge of a blade. When a light beam passes the edge, some rays of the beam are so close to the edge that the atoms of the edge do not appear electric and magnetic neutral. The atomic electric and magnetic forces interact with every passing electric or magnetic photon and exert different resultant force on it. This interaction can cause different bending angles to different passing photons.
Figure (4.3.2) shows that two rays of light meet at the point A of the screen S under the influence of a blade. Since the bending is caused by the edge of the blade, we can suppose B1 is the bending point of ray 1 and B2 is the bending point of ray 2. If we define the difference in path length between B1A and B2A is d, there is
d=B1A-B2A (4.3.2)
At the positions
d=ml (with m=0,1,2…) (4.3.3)
Two electric field quanta or two magnetic field quanta meet. The property of the independent entity field becomes
P=PE+PE=2PE (4.3.4a)
or
P=PB+PB=2PB (4.3.4b)
So, a bright fringe appears on the screen S.
At the positions
d=ml/2 with m=1, 3, 5… (4.3.5)
An electric field quantum and a magnetic field quantum meet. The property is
P=PE+PB=0 (4.3.6)
So, a dark fringe appears on the screen S. In this dark position, photons still exist but their properties can not be detected. This is an important difference between entity field optics and wave optics, in which photons disappeared in the position of a dark fringe.
Based on above concepts, we can rebuild a wave theory of entity field optics to replace the incorrect wave optics.
4.4. Propagation of Independent Entity Field in Transparent Medium
To simplify our discussion, we suppose the medium encountered here is homogeneous, isotropic, transparent and non-source material.
(1) The motion of independent entity field
To eliminate the errors caused by mathematical operations, we introduced symbol P as property to unify electric action E and magnetic action B. Since property P is a scalar, the actions it represented can also be scalars so that independent entity field can be better understood. That is
Thus, the property wave of an independent entity field in a medium can be expressed as
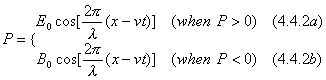
Where v is the wave speed in the medium
(4.4.3)
If ordinary inertial system is chosen, independent entity field can be described as
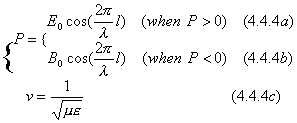
Where v is the light speed in a medium, l is the length of entity field to be measured.
For different media, the values of m and e are different. Even in the same medium, m and e could be different for different frequencies of light. So, light speed is not a constant in a medium.
The ratio between c and v is called index of refraction and is known as n
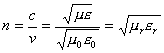(4.4.5)
(2) Electromagnetic energy
According to equation (3.15.12), the energy density of electric photons is
(4.4.6)
And the energy density of magnetic photons is
(4.4.7)
As we know that both E and H have sine-shaped patterns. This means that the energy is not evenly distributed in an independent entity field.
Electromagnetic energy of independent entity field is carried and transferred by each photon. Since an electric photon changes into a magnetic photon, and a magnetic photon changes into an electric photon, the two kinds of photon must have the same energy density
(4.4.8)
The
total energy density of an independent entity field is
(4.4.9)
If S is used to represent energy flux, it can be expressed as
(4.4.10)
Substituting equation (4.4.3) into above equation can get
S=EH (4.4.11)
From equation (4.4.8) we can also get
(4.4.12)
Since both E and
H change between the maximum and zero in different positions, only average
energy flux in one period 
is useful. That is
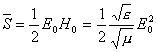(4.4.13)
Where 
is also called the
intensity of light.
(3) Reflection and refraction
If a wave has wavelength l and wave speed v, its wave number k is
(4.4.14)
The period T is
(4.4.15)
Its angular frequency w is
(4.4.16)
Then, the property wave of independent entity field can be expressed as
(4.4.17)
Where r is a vector distance of X-Y plane.
The index of refraction for a media is given by equation (4.4.5) as n=c/v.
Figure (4.4.2) shows an incident light Pi reaches the boundary of two media n1 and n2. It causes a reflected light Pr and a refracted light Pt.
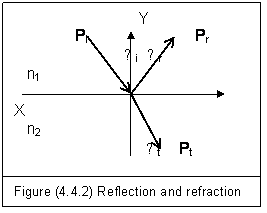
Since an independent entity field must obey law of conservation of energy, we have
Pi=Pr+Pt (4.4.18)
By using equation (4.4.17), it can be changed as
(4.4.19)
To ensure this equation is valid at any time, angular frequency must satisfy
wi=wr=wt=w (4.4.20)
This means that the angular frequency of its property wave is a constant. Meanwhile, to ensure equation (4.4.19) is valid at any position r, there is
kir=krr=ktr (4.4.21)
Relation ki·r=kr·r requires that the horizontal component of ki equals the horizontal component of kr. That is
(4.4.22)
From equation (4.4.14) and equation (4.4.20) we can get
and 
(4.4.23)
Since both incident light and reflected light are traveling in the same medium, they have the same speed
vi=vr (4.4.24)
Thus, equation (4.4.23) can be expressed as
(4.4.25)
Substituting equation (4.4.25) into equation (4.4.22) can get
qi=qr (4.4.26)
This is known as the law of reflection.
Similarly, from relation ki·r=kt·r we have
(4.4.27)
Where kt=w/vt.
Since incident light is traveling in medium n1 with speed vi and refracted light is traveling in n2 with speed vt, equation (4.4.27) can be changed as
(4.4.28)
Both sides multiplied by c yields
(4.4.29)
This is known as the law of refraction.
4.5. Property Wave Superposition
Any electromagnetic wave, including light, is the property wave of an independent entity field with certain wavelength.
As an entity and energy carrier, the whole independent entity field or its photon obeys law of conservation of matter and law of conservation of energy. There is no superposition of light in any circumstance.
As a defined quantity to describe the property change of an independent entity field, its property wave satisfies the superposition principle. This property wave is neither a matter nor energy.
If two rays of independent entity field
and
meet in the space, the total energy or the total number of photons are the sum of the two, but the combined property is the superposition of the two
P=P1+P2 (4.5.1)
Since P is considered as unified electric action E and magnetic action B, it can be expressed as
P=E1+E2-B1-B2 (4.5.2)
If P is considered to represent electric property PE and magnetic property PB, it can be expressed as
P=PE1+PE2-PB1-PB2 (4.5.3)
Both equation (4.5.2) and equation (4.5.3) can be used to decide the superposition in different situations.
Considering two rays of light meet at one point, there are following possibilities of the property superposition:
If the electric property from each ray meets, there is
P=PE1+PE2 (4.5.4)
Superposed property is intensified.
If the magnetic property from each ray meets, there is
P= -(PB1+PB2) (4.5.5)
Superposed property is also intensified.
If at the meeting point P1 has electric property and P2 has magnetic property
P=PE1-PB2 (4.5.6)
Superposed property is weakened.
If at the meeting point P1 has magnetic property and P2 has electric property
P=PE2-PB1 (4.5.7)
Superposed property is also weakened.
In general, for superposition of many rays of light
A very important fact about the property superposition of light is that superposition does not have any permanent effect on each involved ray. Once a ray of light moves away from the meeting point, its property changes back to its original state of electromagnetic wave.
Suppose there are two rays of light that have the same amplitude, the same wavelength and the same frequency, they are known as coherent rays.
The property of each ray can be expressed as
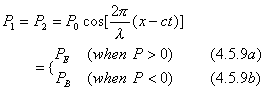
Once
these two rays meet, the superposed property depends on the phase difference f between the
two property waves.
If the phase difference is
f=2pn with n=0,1,2… (4.5.10)
Superposed
property wave is
So, the resultant property wave is the sum of the two.
If the phase difference is
f=pn with n=1,3,5… (4.5.12)
Superposed property wave is
So, property waves of P1 and P2 cancelled each other. At these positions, we cannot detect the two meeting rays by checking their properties. The rays of light still can be detected by checking their photons or energy.
4.6. Diffraction
In diffraction experiment, special experimental methods are used to maximize the effect of property wave of light so that a diffraction pattern can be observed. A simple way of examining diffraction is to partially block a laser beam with a shaving blade. At the back of the blade, there is a diffraction pattern beyond the geometrical edge of the shadow.
There are three important conditions in diffraction experiment.
The first one is to use a coherent light. Otherwise the diffraction pattern cannot be easily observed. One of ideal coherent lights is a laser beam. There are also many other ways of getting coherent light.
The second condition is to split the coherent light into sub-beams so that the sub-beams can have property wave superposition. Some materials to perform this function are: a blade with sharp edge, a metal piece with straight edge, a single slit formed by two straight metal or a small hole of a black paper. One thing in common, they all have clear opaque edge.
The third condition is a screen so that to observe the diffraction pattern.
Figure (4.6.1) is a simplified scheme to show that a single slit can split an incident beam into sub-beams and then cause a diffraction pattern.
In fact, the single slit is a vital condition in diffraction. It sets up heterogeneous electric and magnetic forces to affect the electromagnetic wave of each passing photon. Without the single slit, light travels along straight line and can never produce sub-beams by itself. This is to say that Huygens-Fresnel’s principle is incorrect.
Once the incident beam is split into sub-beams, superposition principle applies to all sub-beams. At the position two or more electric photons (or magnetic photons) meet, a bright spot is obtained. At the position equal numbers of electric photons and magnetic photons meet, a dark spot is created. The whole diffraction pattern is checkered with bright and dark fringes.
Since the function of the single slit is to set up heterogeneous electric and magnetic force fields, an external magnetic force field can also change the condition of the slit so that to change its diffraction pattern. As we can see that the electromagnet-affected diffraction in section 2.7 can be easily explained by entity field theory but can never be explained by Huygens-Fresnel’s principle.
Another significant theoretical difference between entity field theory and Huygens-Fresnel’s principle is about the width of the diffraction pattern.
Entity field theory insists that special relativity is the guideline for light. This means that light must have a constant speed c in free space. When an incident beam passes the single slit, electric and magnetic forces on each passing photon could change its moving direction as shown in figure (4.6.2).
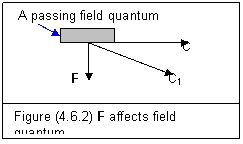
As we can see that the passing photon is moving to the right with speed c while a force F from the slit is driving it down. Under the influence of the F, the passing photon changes its moving direction to c1. There is c1=c according to special relativity. From Newtonian mechanics we know that, due to the photon has speed c, the angle between c1 and c can never reach 900. This means that the forces in slit can never change the direction of a passing photon to 900. Considering the speed c is a very high speed, the direction of a passing photon can only have limited change. The whole diffraction pattern is confined in a certain area not far away from its central symmetric point.
On the contrary, Huygens-Fresnel’s principle believes that light acts like water in a tank. It can create wavelets from any wave front and the wavelets can go to all directions as shown in figure (4.6.3).
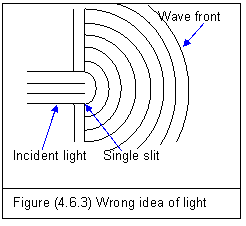
According to this principle, the diffraction pattern should fill up the whole area behind the single slit as the water wave does. Further more, if we adjust the width of the single slit to one wave length of the incident light, the central bright fringe should spread to the whole area behind the single slit.
Checking all kinds of diffraction experiments we can find that any diffraction pattern is confined within a certain area. By using a laser beam as incident light, one can easily observe that there are clear boundaries at both sides of its diffraction pattern. Under no circumstance that diffraction pattern can fill up the diffraction area. Not even close to it.
Since single slit diffraction pattern is directly related to the slit, changing the condition of the slit can change its diffraction pattern. (1) If we use different materials to form single slit, the diffraction pattern will be slightly different due to different atomic structure of the materials. (2) To narrow the width of the slit can cause an intensified force on the incident beam so that its diffraction pattern is spread to a wider area. (3) To apply an extra magnetic force field in the slit can provide extra force on the incident beam so that the diffraction pattern is also spread to a wider area as we demonstrated in section 2.7.
4.7. Interference
Besides diffraction, interference is another way of observing property wave superposition of light. The basic idea of interference is to use a single point light as incident beam and divide it into two beams. These two divided beams are perfect coherent beams. Once these two coherent beams are split into sub-beams, property wave superposition will affect every sub-beam, and then form an interference pattern on the screen.
A typical interference experiment is double slit interference. The arrangement is shown in figure (4.7.1).
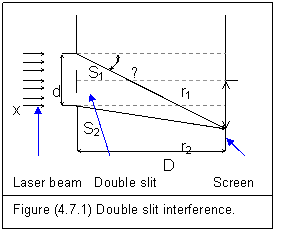
A laser beam is perfect for the incident light. Once the laser beam passes slits s1 and s2, it becomes two coherent light sources. Each of the two is split into sub-beams by the forces in slit. All sub-beams have property wave superposition, and then form interference pattern on the screen.
In figure (4.7.1), the distance between the two slits is d. The distance from double slit to screen is D. There is d<<D. The meeting point of two sub-beams is at x, then the difference in path length is
(4.7.1)
Since d<<D, we have r1+r2»2D. So, the above equation can be simplified as
(4.7.2)
Locations of bright fringes are
Locations of dark fringes are
To explain above interference experiment, there are two important differences between entity field theory and wave optics:
(1) The function of double slit is to divide incident beam into two coherent beams, and then split the two into sub-beams. We don’t need to think light as water in a tank to imagine the so call wavelets of light.
(2) For any double slit interference experiment, interference fringes are confined in a certain area due to the speed of light. Under no circumstance the interference fringe can be seen at 900 as Huygens-Fresnel’s principle predicted.
Any other kinds of interference experiment can be explained similarly and do not have to be repeated here.
4.8. Wrong Concept of Polarization of Light
The concept of polarization of light is based on the wrong ideas that a vector electric field wave (E)and a vector magnetic field wave (B) can form an electromagnetic wave. This electromagnetic wave is also believed to be a transverse wave. The wrong image of light is shown in figure (4.8.1).
To satisfy the
idea of polarization, it is suggested that electric field E itself can form a complete electromagnetic wave. Thus, a polarizer can be used to polarize this vector E.
The so-called polarization can be simply explained by figure (4.8.2).
Figure (4.8.2) The so-called polarization.
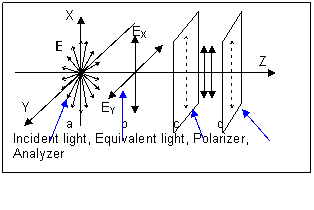
At position a, an incident light moves along Z-axis. Its electric field E is pointing to all directions.
At position b, the same incident light changes itself to an equivalent light, which has only EX and EY. Obviously, this is a correct mathematical change, but is an incorrect physical change.
At position c, a polarizer is used to polarize the light to the direction along X-axis. Only EX can pass through and EY is blocked. So, the incident light is polarized.
At position d, an analyzer is used to check the polarized light. If its polarization direction is along X-axis, polarized light can pass through. If its polarization direction is along Y-axis, polarized light cannot pass.
As we can see that there are three major mistakes here:
(1) Maxwell’s equations (4.1.3) and (4.1.4) require: a moving electric field changes into a magnetic field and a moving magnetic field changes into an electric field. E itself, no matter it is electric field or electric action, cannot form an electromagnetic wave. In fact, E itself does not exist in the physical world at all. Using E to represent an electromagnetic wave is wrong.
(2) If electric field E is only a physical vector, it can be represented by components EX and EY. If electric field E represents an entity as it should be, it cannot be cut into components. We should never mix mathematical calculation with physical reality. This is to say that to resolve E into EX and EY is wrong. If an entity can really be resolved into components, we could resolve a photon into two small photons of different directions.
(3) An anisotropic crystal is assumed to have polarization direction due to its needlelike molecules aligned along one direction. The same anisotropic crystal can be used either as a polarizer to polarize the incident light or as an analyzer to analyze the polarized light. We all know that the basic unit of light is a wavelength. This polarization has to be done in one wavelength level. The size of a molecule is about 10-10 m, and the wavelength of light is about 5000´10-10 m. To think molecule of anisotropic can polarize a light is wrong.
Since the whole theory of polarization is based on the above wrong concepts, to correct any of them can make polarization meaningless. For example, once B is included into electromagnetic wave as it should be, to polarize a light becomes impossible.
We now suppose E is electric field and B is magnetic field as they are suggested in wave optics; and suppose figure (4.8.1) is a correct image of electromagnetic wave. This image requires that a polarized Ex must have a polarized BY with it. The full image of a polarized light coming out of the polarizer should be the one in figure (4.8.3).
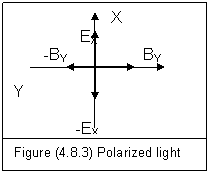
If an anisotropic crystal can polarize the incident light, it must perform following complicated functions: At the direction of X-axis, EX can pass through freely while BX must be blocked completely. At the direction of Y-axis, EY must be blocked while BY must can pass through. This kind of super power is beyond the ability of any natural crystal.
There are many other evidences can be used to prove that there is no such thing as polarization of light. In fact, in entity field theory, this kind of experiment is nothing but property superposition of light.
Experimental fact of anisotropic crystal is that it has different electric characteristics and magnetic characteristics when measured along axis in different directions. This means that, at the surface of the crystal, electric photon and magnetic photon act differently and cause different indices of refraction n1 and n2. Thus, the whole incident light is divided into two perfect coherent lights. This is known as double refraction. Only at the direction n1 and n2 has the same value, there is only one refracted light.
By putting two anisotropic crystals in series, an incident beam can be divided into four coherent sub-beams as shown in figure (4.8.4). (Except from the direction that n1 equals n2.)
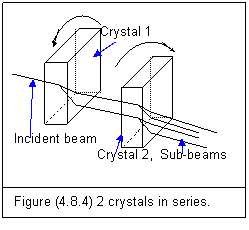
By rotating crystal 1 and crystal 2 about incident light with different angles, we can get different combinations of sub-lights. At certain angles, sub-beams will meet at the back of the crystal 2 and cause a property wave superposition of light.
If the difference in path length for meeting sub-beams is
d=ml where m=1,2,3… (4.8.1)
There is a maximum brightness of transmitted light.
If the difference in path length is
d=ml/2 where m=1,3,5… (4.8.2)
There is a minimum brightness of transmitted light.
In both situations, transmitted light has the same total energy and the same number of total photons. The only difference is the result of the property superposition.
Entity field theory believes that there is a transmitted light at the back of crystal 2 even it could be invisible due to the zero result of its property superposition. The law of conservation of energy or matter is valid at all time.
On the contrary, polarization of light requires that, at the position a dark image is formed at the back of crystal 2, crystal 2 must absorb all transmitted light from crystal 1. This absorbed energy is then disappeared in crystal 2 without any trace and without any proper explanation.
4.9. Photon
In entity field optics, light is photons carrying electromagnetic wave. In the language of entity field theory, light is independent entity field with electromagnetic property wave. It has a constant speed c in free space. Each photon has energy E that depends only on the frequency (or the wavelength) of its property wave. This energy is given by
(4.9.1)
Where h is Planck’s constant. There is h=6.626´10-34 J-s.
The actual length of a photon is half of a wavelength.
The property of photons forms electromagnetic wave in light speed reference system. In ordinary inertial reference system, the property comes with sine-shaped pattern. So, a photon could be an electric photon, a magnetic photon or a photon in the middle state of property change. The period for an electric photon changes into a magnetic photon is half of its one property wave period T.
If a photon hits an electron, the electron can absorb the photon to get its energy. As the result, the photon ceases to exist and transfers its energy to the electron. This energy is used to increase both kinetic energy and virtual photon of the electron. As we understood in QED, a photon is the same material with a virtual photon in a moving electron, they are called entity field here.
In low speed situation (v<<c), the contribution of magnetic energy can be ignored. So, we have
(4.9.2)
Where E0 is the original energy of the electron before the collision; and v is the speed of the electron after the collision.
If the electron is bound with its atom in a material and the binding energy is
Eb=hn0 (4.9.3)
To release this electron, the energy of the striking photon must satisfy
hnłhn0 (4.9.4)
So, equation (4.9.2) can be expressed as
(4.9.5)
Or, in relativistic form
hn=(E-E0)+Eb (4.9.6)
The experiment of releasing electron by photon is known as photoelectric effect. It is direct evidence that light is formed by photons.
From above example we can see that entity field physics can explain any particle experiment of light without any additional condition. So, we can put the so-called wave-particle duality of light in history book now.